RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL

TEMA 3 : RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL

• Ángulo en Posición Normal :Llamado también ángulo en posición canónica o estándar; es aquel ángulo trigonométrico cuyo vértice coincide con el origen del sistema cartesiano, su lado inicial coincide con el semieje positivo de abscisas y su lado se ubicará en cualquier región del plano, siendo el que indique a que cuadrante pertenece dicho ángulo. En el gráfico adjunto por ejemplo : a, b y q son ángulos en posición normal, cumpliéndose: a Î IC; b Î IIC; q Î IIIC.

Ángulos Cuadrantales

Se va a denominar ángulo cuadrantal a aquel ángulo en posición normal cuyo lado final coincide con cualquiera de los semiejes cartesianos. Las medidas de estos ángulos es siempre múltiplo de 90º.

Estos ángulos no pertenecen a cuadrante alguno (fig. 1)

• Ángulos Coterminales 

Son aquellos ángulos en posición normal que tienen el mismo lado final; y su diferencia de medidas es siempre múltiplo de 360º. (fig.2).

• Definición de las razones trigonométricas de un ángulo en Posición Normal

Para definir o hallar las R.T. de un ángulo en posición normal; se debe conocer un punto perteneciente a su lado final.

Veamos su definición gráficamente en el siguiente material:

Ahora visualicemos un ejemplo aplicativo:

Se debe notar que ahora las R.T. pueden tener signo negativo; dependiendo del cuadrante en el que se ubique el ángulo considerado.

* Signos de las R.T.

Dependiendo del cuadrante en el que se ubique un ángulo en posición normal; podemos establecer el siguiente criterio práctico para los signos:

* Propiedad

Las Razones trigonométricas de los ángulos coterminales son respectivamente iguales.

* R.T. de los Ángulos Cuadrantales

Las R.T. de los ángulos cuadrantales principales se calculan con las mismas definiciones aplicadas a cualquier ángulo en posición normal. El resultado se muestra en el siguiente cuadro:

Finalmente a modo de reforzamiento interactivo del presente tema te invito a visualizar el siguiente vídeo para complementar tu aprendizaje de la mejor manera:

RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS

TEMA 2 : RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS

Razones trigonométricas en un triángulo rectángulo

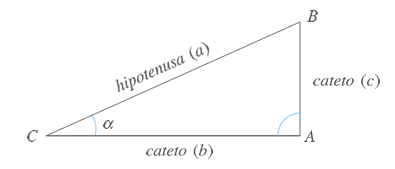A partir de cualquier ángulo agudo α (menor de 90º) es posible construir un triángulo rectángulo ABC como el que puedes apreciar en la siguiente figura.Triángulo rectángulo

Cualquier triángulo rectángulo posee dos ángulos agudos y uno recto.

Teniendo en cuenta dicha figura geométrica y los ángulos formados en cada uno de sus vértices es posible obtener una serie de razones que reciben el nombre de razones trigonométricas conocidas como seno, coseno, tangente, cosecante y cotangente.

seno

El seno de un ángulo agudo α es el cociente entre la longitud del cateto opuesto (c) al ángulo y la longitud de la hipotenusa (a). Se representa como sen(α) o sin(α).

sin(α)= cateto opuestohipotenusa=ca

coseno

El coseno de un ángulo agudo α es el cociente entre la longitud del cateto contiguo (b) al ángulo y la longitud de la hipotenusa (a). Se representa como cos(α).

cos(α)= cateto contiguohipotenusa=ba

tangente

La tangente de un ángulo agudo α es el cociente entre la longitud del cateto opuesto al ángulo (c) y la longitud del cateto opuesto (b). Se representa como tg(α) o tan(α).

tan(α)= cateto opuestocateto contiguo=cb 

cosecante

La cosecante de un ángulo agudo α es la relación inversa del seno, es decir el cociente entre la longitud de la hipotenusa (a) y la longitud del cateto opuesto al ángulo (c). Se representa como cosec(α) o csc(α).

csc(α)=1sin(α)=hipotenusacateto opuesto=ac

secante

La secante de un ángulo agudo α es la relación inversa del coseno es decir, el cociente entre la longitud de la hipotenusa y la longitud del cateto contiguo al ángulo (b). Se representa como sec(α).

sec(α)=1cos(α)=hipotenusacateto contiguo=ab

cotangente

La cotangente de un ángulo agudo α es el cociente entre la longitud del cateto contiguo al ángulo (c) y la longitud del cateto opuesto (b). Se representa como cotg(α) o cot(α).

cotg(α)=1tg(α)=cateto contiguocateto opuesto=bc

A continuación te presento un vídeo donde podemos ver y practicar con algunos ejemplos acerca de la resolución de problemas sobre razones trigonométricas de ángulos agudos: