RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS

TEMA 2 : RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS

Razones trigonométricas en un triángulo rectángulo

A partir de cualquier ángulo agudo α (menor de 90º) es posible construir un triángulo rectángulo ABC como el que puedes apreciar en la siguiente figura.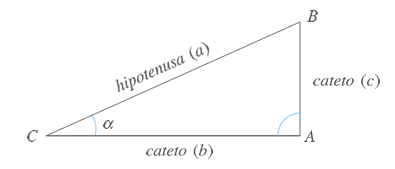Triángulo rectángulo

Cualquier triángulo rectángulo posee dos ángulos agudos y uno recto.

Teniendo en cuenta dicha figura geométrica y los ángulos formados en cada uno de sus vértices es posible obtener una serie de razones que reciben el nombre de razones trigonométricas conocidas como seno, coseno, tangente, cosecante y cotangente.

seno

El seno de un ángulo agudo α es el cociente entre la longitud del cateto opuesto (c) al ángulo y la longitud de la hipotenusa (a). Se representa como sen(α) o sin(α).

sin(α)= cateto opuestohipotenusa=ca

coseno

El coseno de un ángulo agudo α es el cociente entre la longitud del cateto contiguo (b) al ángulo y la longitud de la hipotenusa (a). Se representa como cos(α).

cos(α)= cateto contiguohipotenusa=ba

tangente

La tangente de un ángulo agudo α es el cociente entre la longitud del cateto opuesto al ángulo (c) y la longitud del cateto opuesto (b). Se representa como tg(α) o tan(α).

tan(α)= cateto opuestocateto contiguo=cb 

cosecante

La cosecante de un ángulo agudo α es la relación inversa del seno, es decir el cociente entre la longitud de la hipotenusa (a) y la longitud del cateto opuesto al ángulo (c). Se representa como cosec(α) o csc(α).

csc(α)=1sin(α)=hipotenusacateto opuesto=ac

secante

La secante de un ángulo agudo α es la relación inversa del coseno es decir, el cociente entre la longitud de la hipotenusa y la longitud del cateto contiguo al ángulo (b). Se representa como sec(α).

sec(α)=1cos(α)=hipotenusacateto contiguo=ab

cotangente

La cotangente de un ángulo agudo α es el cociente entre la longitud del cateto contiguo al ángulo (c) y la longitud del cateto opuesto (b). Se representa como cotg(α) o cot(α).

cotg(α)=1tg(α)=cateto contiguocateto opuesto=bc

A continuación te presento un vídeo donde podemos ver y practicar con algunos ejemplos acerca de la resolución de problemas sobre razones trigonométricas de ángulos agudos: